Нахождение Q(z)
Примем, что ось z расположена параллельно длинной оси исследуемого органа. Сделаем гистологические срезы органа в двух перпендикулярных плоскостях: параллельно длинной оси органа (оси z), и перпендикулярно ей. Функцию Q(z) будем искать на изображениях клеток, полученных на срезе, параллельном z. На изображении клетки определим ось z, а перпендикулярно ей от найденного по алгоритму из п. 1. 1 центра клетки построим полярную ось полярной системы координат клетки (рис. 2).
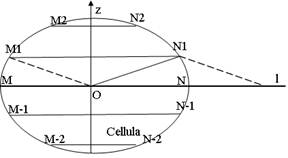
Рис. 2. Нахождение Q(z). Обозначения:
.
.
.
.
.
.
Алгоритм нахождения Q(z) (рис. 2).
1. Относительно полярной системы координат клетки составить интерполяционную формулу функции, описывающей контур сечения клетки, перпендикулярный оси z, по формуле 1. 1 п. 2.
2. 
.
3. 
, так как 
– параллелограмм.
4. 
.
5. Интерполируем функцию Q(z). При этом независимая переменной будет z (по пункту 3), а зависимой величина 
. Тогда интерполяционная формула Ньютона будет иметь вид:
.
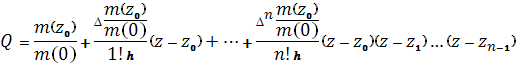Где 
, 
, 
, 
, 
.
6. Определить Q(z) по пунктам 1 - 4 для 20 клеток.
7. Для каждого коэффициента 
построить дискретную функцию 
, где N – это номер клетки в ряду исследованных. Данную функцию можно задать таблицей соответствия значений области определения и области значения. Затем найдем 
(среднее значение коэффициента).
8. Определим между какими клетками лежит найденное среднее значение. Та клетка из найденной пары, к значению которой лежит ближе , считается средней по данному коэффициенту .
9. После того как были найдены средние клетки по всем коэффициентам (их 20, см. пункт 4) находим частоты с которыми клетки становились средними по формуле 
, где p – частота, с – число коэффициентов по которым клетка становилась средней, С=20.
10. Выбираем клетку с наибольшей частотой p, ее функция Q(z) и считается функцией данного клеточного типа.
Также смотрите:
Наиболее распространенные пряные травы нашей территории. Понятие о пряных
травах
Пряные травы в отличие от пряных овощей в большинстве своем дикорастущие, хотя некоторые из них (например, анис, кориандр, тмин, мята, укроп и лаванда) введены человеком в культуру с древнейших времен.
Аромат пряных трав, как правило, усиливается после сушки, но есть ...
Рефлекс
Рефлексом называется реакция организма в ответ на раздражение чувствительных образований — рецепторов, осуществляемая при участии нервной системы. Рецепторы обладают высокой чувствительностью к специфическим для них раздражителям и преобразуют их энергию в процесс нер ...
Самоорганизация
Главной заслугой синергетики считается открытие ею процессов самоорганизации и кооперации в природе - это шаг вперед в познании мира. И хотя авторы синергетики вначале подметили явления самоорганизации только для отдельных физических и химических процессов, но в дальн ...